Unveiling the spread of epidemics involving partial immunity and reinfection: insights from a time-delayed mathematical model

Abstract

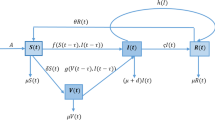
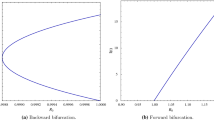
In recent times, several infectious diseases that breakthrough contagiousness in vaccinated people and reinfections in primarily infected counterparts have become more common. In most cases, reinfection occurs as a result of viral mutations. The mutated pathogens may possess alternate modes of transmission, and even the exposure period may vary in some cases. Hence, to gain a deeper understanding of disease transmission dynamics, it becomes eminent to incorporate a dedicated compartment for reinfection within a mathematical model. To account for these vital factors, this research presents an epidemic model that includes a specific compartment for individuals experiencing reinfection. The model also incorporates two separate time delay parameters that account for the incubation periods for the initial infection and the subsequent reinfection. The study reveals that the system exhibits forward bifurcation with respect to the parameter $\beta _1$ in the absence of time delays. However, in the presence of time delay, Hopf bifurcation is identified when the delays exceed corresponding cut-off values. The research further highlights that an extension in the exposure period leads to a rise in the reinfected population, thereby contributing to the persistence of the disease over an extended timeframe. To demonstrate the practical applicability of the proposed model, we have fitted our model with the data of real-time vaccination cases for COVID-19 in India. Notably, the constructed model can be readily adapted for other infectious diseases by selecting appropriate parameter values based on pertinent real-time data. The theoretical results are validated via numerical simulation.

Appendices

Appendix 1

$$\begin{aligned} \alpha _{11}&=\xi _4+\phi _1+\phi _2+\phi _3+\phi _4,\\ \alpha _{12}&=\xi _4\phi _1+\xi _4\phi _2+\phi _1\phi _2+\xi _4\phi _3+\phi _2\phi _3+\phi _5+\xi _4\phi _4\\&~~~+\phi _1\phi _4+\phi _2\phi _4+\phi _3\phi _4,\\ \alpha _{13}&=\phi _5(\xi _4+\phi _2+\phi _4)+\xi _4(\phi _1\phi _2+\phi _2\phi _3+\phi _1\phi _4\\&~~~+\phi _2\phi _4+\phi _3\phi _4)+\phi _2\phi _4(\phi _1+\phi _3),\\ \alpha _{14}&=\phi _5(\xi _4\phi _2+\xi _4\phi _4+\phi _2\phi _4)+\xi _4\phi _2\phi _4(\phi _1+\phi _3),\\ \alpha _{15}&=\xi _4\phi _2\phi _4\phi _5,\\ b_{11}&=\eta _2-\eta _1,\\ b_{12}&=(\eta _2-\eta _1)(\xi _4+\phi _3+\phi _4)+\eta _2\phi _1-\eta _1\phi _2,\\ b_{13}&=\phi _5+\eta _2\xi _4(\phi _1+\phi _3+\phi _4)-\eta _1(\xi _4(\phi _2+\phi _3+\phi _4)\\&~~~+(\phi _2\phi _3+\phi _2\phi _4+\phi _3\phi _4))+\eta _2\phi _4(\phi _1+\phi _3),\\ b_{14}&=\eta _2(\xi _4\phi _5+\phi _4\phi _5+\xi _4\phi _4(\phi _1+\phi _3))\\&~~~-\eta _1(\xi _4(\phi _2\phi _3+\phi _3\phi _4+\phi _2\phi _4)-\phi _2\phi _3\phi _4),\\ b_{15}&=\xi _4\phi _4(\eta _2\phi _5-\eta _1\phi _2\phi _3),\\ c_{11}&=\eta _3-\eta _4,\\ c_{12}&=r\eta _4+\eta _3(\xi _4+\phi _1+\phi _2+\phi _3)\\ &\quad -\eta _4(\phi _1+\phi _2+\phi _3+\phi _4),\\ c_{13}&=(\eta _3-\eta _4)(\phi _5+\phi _2(\phi _1+\phi _3))\\&~~~+(\phi _1+\phi _2+\phi _3)(r\eta _4+\eta _3\xi _4-\eta _4\phi _4),\\ c_{14}&=(r\eta _4+\eta _3\xi _4)(\phi _1\phi _2+\phi _2\phi _3+\phi _5)\\&~~~-\eta _4(\phi _5(\phi _2+\phi _4)+\phi _2\phi _4(\phi _1+\phi _3))+\eta _3\phi _2\phi _5,\\ c_{15}&=\phi _5\phi _2(r\eta _4+\eta _3\xi _4-\eta _4\phi _4),\\ f_{11}&=\eta _1(\eta _3-\eta _4)+\eta _2\eta _4,\\ f_{12}&=r\eta _4(\eta _1-\eta _2)+\eta _1\eta _3(\xi _4+\phi _2+\phi _3)\\&~~~-\eta _1\eta _4(\phi _2+\phi _3+\phi _4)+\eta _2\eta _4(\gamma +\phi _1+\phi _3+\phi _4),\\ f_{13}&=\eta _2\eta _4(\phi _5+(\gamma -r)(\phi _1+\phi _3)+\phi _4(\phi _1+\phi _2)-\rho \omega _2)\\&~~~+\eta _1\eta _4(r(\phi _2+\phi _3)-(\phi _2\phi _3+\phi _2\phi _4+\phi _3\phi _4))\\&~~~+\eta _1\eta _3(\xi _4\phi _2+\xi _4\phi _3+\phi _2\phi _3),\\ f_{14}&=r\eta _2\eta _4(\phi _1\phi _3+\rho \omega _1)+\eta _2\eta _4\psi _4(\gamma +\phi _4)\\&~~~+\eta _1\eta _4\phi _2\phi _3(r-\phi _4)+\phi _2(\eta _1\eta _3\xi _4\phi _3-\eta _2\eta _4\rho \omega _2),\\ \eta _1&=\beta _1(I_1^*+I_2^*)/N^*,\\ \eta _2&=\beta _1S^*/N^*,\\ \eta _3&=\beta _2C^*/N^*,\\ \eta _4&=\beta _2(I_1^*+I_2^*)/N^*. \end{aligned}$$

Appendix 2

Proof of Theorem 3(c)

For $\tau _1=0$, the Eq. (11) becomes

$$\begin{aligned}&\lambda ^5+A_{21}\lambda ^4+A_{22}\lambda ^3+A_{23}\lambda ^2+A_{24}\lambda +A_{25}\nonumber \\&-e^{-\lambda \tau _2}(A_{26}\lambda ^4+A_{27}\lambda ^3+A_{28}\lambda ^2+A_{29}\lambda +A_{20}), \end{aligned}$$

(19)

where

$$\begin{aligned} A_{21}&=\alpha _{11}-b_{11},\quad A_{22}=\alpha _{12}-b_{12},\quad A_{23}=\alpha _{13}-b_{13},\\ A_{24}&=\alpha _{14}-b_{14},\quad A_{25}=\alpha _{15}-b_{15},\quad A_{26}=c_{11},\\ A_{27}&=c_{12}+f_{11},\quad A_{28}=c_{13}+f_{12},\quad A_{29}=c_{14}+f_{13},\\ A_{20}&=c_{15}+f_{14}.\quad \end{aligned}$$

If $\lambda =im$ is a root of the Eq. (19), we obtain

$$\begin{aligned} m^{10}+P_{61}m^8+P_{62}m^6+P_{63}m^4+P_{64}m^2+P_{65}=0. \end{aligned}$$

(20)

Where,

$$\begin{aligned} P_{61}&=A_{21}^2-2A_{22}-A_{26}^2,\\ P_{62}&=A_{22}^2-2A_{21}A_{23}+2A_{24}-A_{27}^2+2A_{26}A_{28},\\ P_{63}&=A_{23}^2+2A_{22}A_{24}-2A_{20}A_{26}-A_{28}^2+2A_{27}A_{29},\\ P_{64}&=A_{24}^2+2A_{20}A_{28}-A_{29}^2,\\ P_{65}&=-A_{20}^2.\\ \end{aligned}$$

Let $m^2=t$. Then Eq. (20) becomes

$$\begin{aligned} t^5+P_{61}t^4+P_{62}t^3+P_{63}t^2+P_{64}t+P_{65}=0. \end{aligned}$$

(21)

Consider that Hypothesis 2: $t_{20}$ is a positive root of Eq. (21). Then Eq. (20) has a positive root $m_{20}=\sqrt{t_{20}}$ and further we obtain the following

$$\begin{aligned} \tau _{20}=\frac{1}{m_{20}}\arcsin \left( \frac{M_{21}M_{23}+M_{22}M_{24}}{M_{21}^2+M_{22}^2}\right) \end{aligned}$$

with

$$\begin{aligned} M_{21}&=A_{26}m^4-A_{28}m^2+A_{20},\\ M_{22}&=A_{27}m^3-A_{29}m,\\ M_{23}&=-A_{22}m^3-A_{24}m-m^5,\\ M_{24}&=-A_{21}m^4+A_{23}m^2. \end{aligned}$$

Also, we obtain, Re$[d\lambda /d\tau _2]^{-1}_{\lambda =im_{20}}\ne 0$ if $\left. \varUpsilon _2^{'}(t)=\frac{d\varUpsilon _2(t)}{dt}\right| _{t=t_{20}}\ne 0$ holds, where $\varUpsilon _2(t)=t^5+P_{61}t^4+P_{62}t^3+P_{63}t^2+P_{64}t+P_{65}.$ Thus according to the Hopf bifurcation theorem in [45], the system undergoes Hopf bifurcation whenever the above transversality condition holds. $\hfill\square$

Proof of Theorem 3(d)

When $\tau _1=\tau _2=\tau >0$, the Eq. (11) becomes

$$\begin{aligned}&\lambda ^5+\alpha _{11}\lambda ^4+\alpha _{12}\lambda ^3+\alpha _{13}\lambda ^2+\alpha _{14}\lambda +\alpha _{15}\nonumber \\&-e^{-\lambda \tau }\left( A_{31}\lambda ^4+A_{32}\lambda ^3+A_{33}\lambda ^2+A_{34}\lambda +A_{35}\right) \nonumber \\&-e^{-2\lambda \tau }\left( f_{11}\lambda ^3+f_{12}\lambda ^2+f_{13}\lambda +f_{14}\right) =0. \end{aligned}$$

(22)

where

$$\begin{aligned}&A_{31}=b_{11}+c_{11},\quad A_{32}=b_{12}+c_{12},\quad A_{33}=b_{13}+c_{13},\\&A_{34}=b_{14}+c_{14},\quad A_{35}=b_{15}+c_{15}.\quad \end{aligned}$$

Multipliying $e^{\lambda \tau }$ on both sides of Eq. (22), we get the following

$$\begin{aligned}&e^{\lambda \tau }\left( \lambda ^5+\alpha _{11}\lambda ^4+\alpha _{12}\lambda ^3+\alpha _{13}\lambda ^2+\alpha _{14}\lambda +\alpha _{15}\right) \nonumber \\&-(A_{31}\lambda ^4+A_{32}\lambda ^3+A_{33}\lambda ^2+A_{34}\lambda +A_{35})\nonumber \\&-e^{-\lambda \tau }(f_{11}\lambda ^3+f_{12}\lambda ^2+f_{13}\lambda +f_{14})=0. \end{aligned}$$

(23)

Let $\lambda =im$ is a root of the Eq. (23), then we get the following equations

$$\begin{aligned} M_{31}\cos (m\tau )+M_{32}\sin (m\tau )&=M_{33},\\ M_{34}\cos (m\tau )+M_{35}\sin (m\tau )&=M_{36}. \end{aligned}$$

Where,

$$\begin{aligned} M_{31}&=m^5-\alpha _{12}m^3+\alpha _{14}m+f_{11}m^3-f_{13}m,\\ M_{32}&=\alpha _{11}m^4-\alpha _{13}m^2+\alpha _{15}-f_{12}m^2+f_{14},\\ M_{33}&=A_{34}m,\\ M_{34}&=\alpha _{11}m^4-\alpha _{13}m^2+\alpha _{15}+f_{12}m^2-f_{14},\\ M_{35}&=-m^5+\alpha _{12}m^3-\alpha _{14}m+f_{11}m^3-f_{13}m,\\ M_{36}&=A_{31}m^4-A_{32}m^3-A_{33}m^2+A_{35}. \end{aligned}$$

From the above set of equations, we obtain,

$$\begin{aligned} \sin (m\tau )=\frac{\widehat{M_1}}{\widehat{M_3}},\qquad \cos (m\tau )=\frac{\widehat{M_2}}{\widehat{M_3}} \end{aligned}$$

(24)

with,

$$\begin{aligned} \widehat{M_1}&=M_{31}M_{36}-M_{33}M_{34},\\ \widehat{M_2}&=-M_{32}M_{36}+M_{33}M_{35},\\ \widehat{M_3}&=M_{31}M_{35}-M_{32}M_{34}. \end{aligned}$$

Where we obtain the following equation,

$$\begin{aligned} \widehat{M_3}^2=\widehat{M_1}^2+\widehat{M_2}^2. \end{aligned}$$

(25)

We consider the Hypothesis 3: $m_{0}$ is a positive root of Eq. (25). If the Hypothesis 3 holds, then, we arrive at the following

$$\begin{aligned} \tau _{0}=\frac{1}{m_{0}}\arcsin \left( \frac{M_{31}M_{36}-M_{33}M_{34}}{M_{31}M_{35}-M_{32}M_{34}}\right) . \end{aligned}$$

Following in similar manner as in the above cases, we see that Re$[d\lambda /d\tau ]^{-1}_{\lambda =im_{30}}\ne 0$ if $\left. \varUpsilon _3^{'}(t)=\frac{d\varUpsilon _3(t)}{dt}\right| _{t=t_{0}}\ne 0$ holds, where $\varUpsilon _3(t)=t^5+P_{71}t^4+P_{72}t^3+P_{73}t^2+P_{74}t+P_{75}.$ with $P_{71}=-{A_{{31}}}^{2}+2\,{\alpha _{{11}}}^{2}-4\,\alpha _{{12}}$, $P_{72}=2M_{{33}} \left( \alpha _{{15}}-f_{{14}} \right) \left( \alpha _{{14} }-f_{{13}} \right) A_{{35}}+2\, \left( \alpha _{{15}}+f_{{14}} \right) A_{{35}}M_{{33}} \left( -\alpha _{{14}}-f_{{13}} \right)$, $P_{73}=- \left( \alpha _{{14}}-f_{{13}} \right) A_{{33}}+ \left( -\alpha _{{12} }+f_{{11}} \right) A_{{35}}$, $P_{74}=- \left( \alpha _{{15}}+f_{{14}} \right) A_{{31}}+ \left( -\alpha _{{13} }-f_{{12}} \right) A_{{33}}-\alpha _{{11}}A_{{35}}$ and $P_{75}=2\,\alpha _{{11}} \left( -\alpha _{{13}}+f_{{12}} \right)$. Thus according to the Hopf bifurcation theorem in [45], we determine the existence of Hopf bifurcation whenever the Hypothesis 3 and the above transversality condition holds. $\hfill\square$

Proof of Theorem 3(e)

When $\tau _1\ge 0$ and $\tau _2\in (0,\tau _{20})$. Letting $\lambda =im$ in Eq. (11) and simplifying further we obtain

$$\begin{aligned} M_{41}\cos (m\tau _1)+M_{42}\sin (m\tau _1)=M_{43},\\ -M_{42}\cos (m\tau _1)+M_{41}\sin (m\tau _1)=M_{44}. \end{aligned}$$

Where,

$$\begin{aligned} M_{41}&=\sin (m\tau _{2}) \left( -{m}^{2}f_{{12}}+f_{{14}} \right) +b_{{12}}{m}^{3}-b_{{ 14}}m\\&~~~-\cos (m\tau _2) \left( -{m}^{3}f_{{11}}+mf_{{13}} \right) ,\\ M_{42}&=b_{{11}}{m}^{4}-b_{{13}}{m}^{2}+b_{{15}}+\cos (m\tau _{2}) \left( -{m}^{2}f_{{12 }}+f_{{14}} \right) \\&~~~+\sin (m\tau _2) \left( -{m}^{3}f_{{11}}+mf_{{13}} \right) ,\\ M_{43}&={m}^{4}c_{{11}}\sin (m\tau _2)+{m}^{5}+{m}^{3}\cos (m\tau _2)c_{{12}}\\&~~~-{m}^{3}\alpha _{{ 12}}-{m}^{2}c_{{13}}\sin (m\tau _2)-m\cos (m\tau _2)c_{{14}}\\&~~~+m\alpha _{{14}}+c_{{15}}\sin (m\tau _2),\\ M_{44}&=\left( -\cos (m\tau _2)c_{{11}}+\alpha _{{11}} \right) {m}^{4}+\sin (m\tau _{2})c_{{12}} {m}^{3}\\&~~~+ \left( \cos (m\tau _2)c_{{13}}-\alpha _{{13}} \right) {m}^{2}-\sin (m\tau _{2})c _{{14}}m\\&~~~-\cos (m\tau _2)c_{{15}}+\alpha _{{15}}. \end{aligned}$$

By simple calculation, we obtain the following characteristic equation

$$\begin{aligned} m^{10}+P_{81}t^4+P_{82}t^3+P_{83}t^2+P_{84}t+P_{85}=0, \end{aligned}$$

(26)

where,

$$\begin{aligned} P_{81}&=2c_{11}\sin (m\tau _2),\\ P_{82}&={c_{{11}}}^{2}-2\,\alpha _{{11 }}c_{{2}}c_{{11}}+{\alpha _{{11}}}^{2}-{b_{{11}}}^{2}\\&~~~+2\,\cos (m\tau _2)c_{{12} }-2\,\alpha _{{12}}, \\ P_{83}&=-2\,\sin (m\tau _2) \left( \alpha _{{11}}c_{{14}}-\alpha _{{12}}c_{{13}}+\alpha _ {{13}}c_{{12}}-\alpha _{{14}}c_{{11}}\right. \\&~~~\left. +b_{{11}}f_{{13}}-b_{{12}}f_{{12}} +b_{{13}}f_{{11}}-c_{{15}} \right) , \\ P_{84}&=2\,\sin (m\tau _2) \left( \alpha _{{14}}c_{{15}}-\alpha _{{15}}c_{{14}}+b_{{14}} f_{{14}}-b_{{15}}f_{{13}} \right) , \\ P_{85}&=2\,\sin (m\tau _2) \left( \alpha _{{11}}c_{{12}}-\alpha _{{12}}c_{{11}}+b_{{11}} f_{{11}}-c_{{13}}. \right) \end{aligned}$$

We consider the Hypothesis 4: $m_{100}$ is a positive root of Eq. (30). If the Hypothesis 4 holds, then, we arrive at the following

$$\begin{aligned} \tau _{100}=\frac{1}{m_{100}}\arcsin \left( \frac{M_{41}M_{43}+M_{42}M_{44}}{M_{41}^2+M_{42}^2}\right) . \end{aligned}$$

Following in similar manner as in the above cases, we see that Re$[d\lambda /d\tau ]^{-1}_{\lambda =im_{100}}\ne 0$ if $\left. \varUpsilon _4^{'}(t)=\frac{d\varUpsilon _4(t)}{dt}\right| _{t=t_{0}}\ne 0$ holds, where $\varUpsilon _4(t)=t^5+P_{81}t^4+P_{82}t^3+P_{83}t^2+P_{84}t+P_{85}$. Thus according to the Hopf bifurcation theorem in [45], we determine the existence of Hopf bifurcation whenever the Hypothesis 4 and the above transversality condition holds. $\hfill\square$