1 Introduction

Cycling science is a lucrative and competitive industry, in which small advantages are often the difference between winning and losing. For example, the 2018 Tour de France was won by a margin of less than one minute for a total race time of more than 86 h [10]. Improvements in performance typically require the combined expertise of a wide range of specialists, including sports scientists, engineers, and dieticians. In addition, mathematics can provide a fundamental underpinning for the race dynamics and strategy, to complement the results of more sophisticated analyses such as computational fluid dynamics simulations.

Long-distance cycle races, such as a stage of the Tour de France, typically follow a prescribed pattern: riders cycle together as a main group, or peloton, for the majority of the race before a solo rider or small group of riders makes a break from the peloton, usually relatively close to the finish line. The main reason for this behaviour is that cycling in a group reduces the air resistance that is experienced by a cyclist. With energy savings of up to around a third when cycling in the peloton compared with riding solo [8], it is energetically favourable to stick with the main field for the majority of the race. However, if a cyclist wishes to win a race or a Tour stage then they must decide on when to make a break. In doing so, the rider must provide an additional pedal force to offset the effects of air resistance that would otherwise be mitigated by riding in the peloton. However, the cyclist will not be able to sustain this extra force indefinitely, with fatigue effects coming into play. As a result, a conflict emerges: if the cyclist breaks away too soon then they risk fatigue effects kicking in before the finish line and being caught by the peloton. On the other hand, if the cyclist breaks too late then they reduce their chance of a large winning margin.

The mathematics of drag and air resistance in the context of cycling science is well known and has led to many studies considering strategies for minimizing this drag reduction, ranging from cycling behind a rider (see, for example, [3] for a summary) to the foot positioning on downhill sections  [6]. Strategies for short-distance races have been examined (see, for example, [9]) in which minute changes in tactics can be the difference between winning and losing. In long-distance races, many more tactics come into play, such as pacing [5, 18]. In such races, while drag reduction plays a much more important role, the combination of the knowledge of drag with strategies for winning a long-distance race are much less common, at least in the public literature.

In this paper we consider, for a given course profile and rider statistics, the optimum time to break away, which maximizes the time difference between the rider finishing and the peloton crossing the finish line. To answer this question we derive a mathematical model for cycling that captures the advantage of riding in the peloton to reduce aerodynamic drag and the physical limitations (due to fatigue) on the force that can be provided by the leg muscles.

We begin in Sect. 2 by forming a mathematical model for the motion of a single rider, which is extended in Sect. 3 to describe a group of cyclists and a breakaway rider, as seen in professional cycle races. The model for a single rider is derived by considering the forces acting on a cyclist by appealing to Newton’s Second Law. To make analytical progress, we use an asymptotic expansion that exploits the fact that variations from a mean course gradient are typically small. We then examine the validity of these solutions by comparing them to numerical calculations of the full mathematical model that do not rely on the assumption of small undulations. The asymptotic solutions also provide a method to draw direct relationships between the values of physical parameters and the time taken to cover a set distance.

The physiological factors that limit the force that muscles are able to provide are then explored in Sect. 4. We assume that the concentration of potassium ions in the muscle cells is a strong factor in the fatigue of the muscles after a period of exertion, and we form equations to model the evolution of force output over time. This is applied to a breakaway situation to understand how the muscles respond after a rider exerts a force above their sustainable level.

Finally, in Sect. 5, we seek an optimal breakaway strategy using the framework derived. We model a race situation with the main field of riders benefiting from a drag reduction and a breakaway rider applying a higher pedal force which decays with time and find the optimal position along a course to break away from the peloton, using the asymptotic solutions for both a constant breakaway force and accounting for fatigue effects.

2 Mathematical model for a single rider

2.1 Governing equation for the rider motion

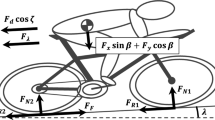
We begin by forming a mathematical model for the one-dimensional motion of a single rider. We characterize the rider’s motion by the distance travelled along the course, \(\hat{x}\), at time \(\hat{t}\), and the course undulations by the angle of incline, \({\theta }={\theta }(\hat{x})\) (see Fig. 1). Note we use hats to denote dimensional quantities and, for future reference, variables without hats will be dimensionless.

Newton’s Second Law, \(\hat{F}_{\text {tot}} = \hat{m}\text {d}^2\hat{x}/\text {d}\hat{t}^2\), describes the rider’s motion in the direction of travel, where \(\hat{m}\) denotes the mass of the rider. The force \(\hat{F}_{\text {tot}}\) is the total component of force acting in the direction of travel. Since we are considering one-dimensional motion we ignore any forces that would arise when turning a corner such as the centripetal force. The role of corners is more important in track cycling and the advantages of leaning into corners is considered in [19]. The forces acting on a rider that we will consider are as follows:

  • The force due to gravity, \(\hat{m}\hat{g}\sin {\theta }(\hat{x})\), where \(\hat{g}\) denotes acceleration due to gravity.

  • The frictional force, \(\hat{F}_{\text {f}}\), capturing the resistance of the tyres with the road and the sum of all mechanical resistances including from the chain and wheel bearings. Here we assume that \(\hat{F}_{\text {f}}\) is constant, as is also assumed by Martin [13] and Pivit [15].

  • The phenomenological drag force \(\hat{F}_{\text {D}}=\frac{1}{2}\hat{\rho }c_{\text {D}} \hat{A} (\text {d}\hat{x}/\text {d}\hat{t})^2\), where \(\hat{\rho }\) is the density of air, \(c_{\text {D}}\) is a drag coefficient, and \(\hat{A}\) is the frontal area of the bike and rider. This form of the drag law assumes that the air is stationary, but readily generalizes to allow for wind by replacing \((\text {d}\hat{x}/\text {d}\hat{t})^2\) with \((\text {d}\hat{x}/\text {d}\hat{t}-\hat{v}_w)^2\), where \(\hat{v}_w\) is the air velocity in the positive \(\hat{x}\) direction (\(\hat{v}_w>0\) corresponds to a tailwind and \(\hat{v}_w<0\) corresponds to a headwind). In what follows we will assume that \(\hat{v}_{w} \equiv 0\). While the effects of crosswinds can be important, with riders forming echelons to shield each other from crosswinds, we will neglect this effect here as this plays a small role on the forward motion of riders

  • The pedalling force, \(\hat{F}_{\text {p}}\), which could depend in general on \(\hat{x}\), \(\text {d}\hat{x}/\text {d}\hat{t}\) and \(\hat{t}\) to reflect a varying power output. We will begin by assuming \(\hat{F}_{\text {p}}\) to be constant, which provides a good approximation for relatively constant speeds. In this case the power output, \(\hat{F}_{\text {p}}\text {d}\hat{x}/\text {d}\hat{t}\), is constant when travelling at constant speed and increases linearly with speed. We relax the assumption of constant pedal force in Sect. 4.

Fig. 1
figure 1

Schematic illustrating the coordinate set-up and forces acting on the rider

Full size image

In summary, Newton’s Second Law then provides us with the second-order differential equation for the rider’s displacement:

$$\begin{aligned} \hat{m}\frac{\text {d}^2\hat{x}}{\text {d}\hat{t}^2} = \hat{F}_{\text {p}} - \hat{F}_{\text {f}} - \frac{1}{2}\hat{\rho } c_{\text {D}} \hat{A} \left( \frac{\text {d}\hat{x}}{\text {d}\hat{t}}\right) ^2 - \hat{m}\hat{g}\sin {\theta }(\hat{x}). \end{aligned}$$
(1)

We solve the model (1) for \(\hat{t} \ge 0\), where \(\hat{t}=0\) corresponds to the time at which we are interested in modelling the race behaviour. For instance, this may be the point in the course at which the peloton has settled into a steady pace and riders are beginning to think about making a break. Without loss of generality we impose the initial conditions

$$\begin{aligned} \hat{x}(0)&= 0, \end{aligned}$$
(2a)
$$\begin{aligned} \frac{\text {d}\hat{x}(0)}{\text {d}\hat{t}}&= \hat{v}_i, \end{aligned}$$
(2b)

which corresponds to specifying the origin of \(\hat{x}\), and the rider velocity at that time, \(\hat{v}_i\).

2.2 Non-dimensionalization

We non-dimensionalize Eq. (1) to elucidate the dependence of the model on the physical parameters. Specifically, we make the following choices:

$$\begin{aligned}&\hat{x}=\hat{L}{x}, \quad \hat{t}=\hat{T}{t}, \quad \hat{m}=\hat{M}{m}, \quad \hat{v}_i=\frac{\hat{L}}{\hat{T}}v_i, \nonumber \\&\hat{F}_{\text {f}}=\hat{M}\hat{g}F_{\text {f}}, \qquad \hat{F}_{\text {D}}=\hat{M}\hat{g}F_{\text {D}}, \qquad \hat{F}_{\text {p}}=\hat{M}\hat{g}F_{\text {p}}, \qquad \end{aligned}$$
(3)

where \(\hat{L}\), \(\hat{T}\) and \(\hat{M}\) are characteristic scales that will be determined. Using (3) we find that (1) then becomes

$$\begin{aligned} m\frac{\text {d}^2 {x}}{\text {d}{t}^2} = \frac{\hat{T}^2\hat{g}}{\hat{L}}(F_{\text {p}} - F_{\text {f}}) - \frac{\hat{\rho }c_{\text {D}} \hat{A} \hat{L}}{2\hat{M}} \left( \frac{\text {d}{x}}{\text {d}{t}} \right) ^2 - \frac{m\hat{g}\hat{T}^2}{\hat{L}}\sin {\theta }({x}), \end{aligned}$$
(4)

where \({\theta }({x})={\theta }(\hat{x}/\hat{L})\).

We choose to balance the final term with the acceleration to allow us to later take advantage of the final term being small, which gives \(\hat{T}=\sqrt{\hat{L}/\hat{g}}\). We choose \(\hat{M}\) to be the average mass of the riders (in a race, for example) and choose \(\hat{L}=2\hat{M}/\hat{\rho } c_{\text {D}} \hat{A}\) to balance the drag term. In this section we set \(F_{\text {p}}=F_{\text {s}}\), where \(F_{\text {s}}\) is a constant pedal force that can be sustained indefinitely. In later sections we consider a more complex form for the pedal force. We also simplify by defining the dimensionless constant force \({F_0=F_{\text {s}}-F_{\text {f}}}\) to obtain the dimensionless governing equation

$$\begin{aligned} m\ddot{x} = F_0 - \dot{x}^2 - m\sin \theta (x), \end{aligned}$$
(5)

where a dot denotes differentiation with respect to time.

2.3 Solution for a flat course

Equation (5) can be solved for a flat course (\(\theta (x)=0\)) by substituting \(v=\dot{x}\) and rearranging to give the integral equation

$$\begin{aligned} \int _{v_i}^v \frac{m}{F_0 - \tilde{v}^2} \text {d}\tilde{v} = t. \end{aligned}$$
(6)

Solving equation (6) gives two forms of solution, depending on the sign of \(F_0-v_i^2\):

$$\begin{aligned} \dot{x}(t)&= \left\{ \begin{array}{ll} \sqrt{F_0}\tanh \left( \xi _0(t)\right) \ &{}\quad \text {for } v_i< \sqrt{F_0}, \\ \sqrt{F_0}\coth \left( \bar{\xi _0}(t)\right) &{}\quad \text {for } v_i>\sqrt{F_0}, \end{array}\right. \end{aligned}$$
(7a)
$$\begin{aligned} x(t)&= \left\{ \begin{array}{ll} m\log \cosh \left( \xi _0(t)\right) + \sigma _0 &{}\quad \text {for}\,\, v_i< \sqrt{F_0},\\ m\log \sinh \left( \bar{\xi }_0(t)\right) + \sigma _0 &{}\quad \text {for } v_i>\sqrt{F_0}, \end{array}\right. \end{aligned}$$
(7b)

where

$$\begin{aligned} \xi _0(t)&=\sqrt{F_0}t/m+{\text {artanh}}\left( v_i/\sqrt{F_0} \right) ,\\ \bar{\xi }_0(t)&=\sqrt{F_0}t/m+{\text {artanh}}\left( \sqrt{F_0}/v_i \right) ,\\ \text {and}\quad \sigma _0&=m/2\log \left| {v_i^2}/{F_0} - 1 \right| . \end{aligned}$$

Here we have assumed that \(F_0>0\), meaning the pedalling force provided is at least high enough to overcome the friction force, otherwise our model would predict that the rider would eventually come to a stop, which is a case that we are not concerned with here.

2.4 Approximation for a weakly undulating course

We now seek a solution for a course where \(\theta\) varies by a small amount about a mean value, \(\alpha\). We expect this to apply for real courses since they can be divided into sections that have an approximately constant slope, and within these sections the variation of the angle \(\theta\) about this slope will generally be small. We therefore write

$$\begin{aligned} {\theta (x)=\alpha +\varepsilon f(x)}, \end{aligned}$$
(8)

where \(0<\varepsilon \ll 1\) and \(f=O(1)\), and expand the displacement as a power series in \(\varepsilon\),

$$\begin{aligned} x = x_0 + \varepsilon x_1 + \varepsilon ^2 x_2 + \cdots \ . \end{aligned}$$
(9)

Substituting (8) and (9) into (5) and the initial conditions (2), and then equating orders of \(\varepsilon\) provides the differential equations and initial conditions

$$\begin{aligned}&O(1): \qquad {\left\{ \begin{array}{ll} m\ddot{x}_0 = F_0 - \dot{x}_0^2 - m\sin \alpha , \\ x_0(0) = 0, \quad \dot{x}_0(0) = v_i, \end{array}\right. } \end{aligned}$$
(10a)
$$\begin{aligned}&O(\varepsilon ): \qquad {\left\{ \begin{array}{ll} m\ddot{x}_1 = -2\dot{x}_0\dot{x}_1 - m f(x_0)\cos \alpha , \\ x_1(0) = 0, \quad \dot{x}_1(0) = 0. \end{array}\right. } \end{aligned}$$
(10b)

Equation (10a) is of the same form as the flat-course Eq. (5), with \(F_0\) replaced by \(F_\alpha :=F_0-m\sin \alpha\), which we again assume to be positive so that the pedal force is sufficient to overcome the friction and gravitational forces. The form of the solution depends on the sign of \(F_\alpha -v_i^2\). Here we will suppose that \(F_\alpha>v_i^2\) so that the driving force generates acceleration at \(t=0\), but acknowledge that analogous solutions to that shown in Sect. 2.3 exist for \(F_\alpha <v_i^2\). The leading-order solution is then

$$\begin{aligned} \dot{x}_0(t)&= \sqrt{F_\alpha }\tanh \left( \xi _\alpha (t)\right) , \end{aligned}$$
(11a)
$$\begin{aligned} x_0(t)&= m\log \cosh \left( \xi _{\alpha }(t)\right) + \sigma _\alpha , \end{aligned}$$
(11b)

where

$$\begin{aligned} \xi _{\alpha }(t)&=\sqrt{F_{\alpha }}t/m+{{\mathrm{artanh}}}\left( v_i/\sqrt{F_\alpha } \right) \\ \text {and}\quad {\sigma _\alpha }&= m/2\log \left| v^2_{i} / F_{\alpha } - 1\right| . \end{aligned}$$

At \(O(\varepsilon )\), equation (10b) yields a linear second-order differential equation in \(\dot{x}_1\), with \(x_0(t)\), f(x) and \(\alpha\) known, and so can be solved by finding an integrating factor. This provides the correction to the velocity and displacement due to the undulations,

$$\begin{aligned} \begin{array}{ll} \dot{x}_1(t)&= -\cos \alpha\,\, {{\mathrm{sech}}}^2\left( \xi _\alpha (t)\right) \int _0^t \cosh ^2\left( \xi _\alpha (s)\right) f(x_0(s)) {\text {d}}s, \end{array} \end{aligned}$$
(12a)
$$\begin{aligned} x_1(t) = -\cos \alpha \int _0^t {{\mathrm{sech}}}^2\left( \xi _\alpha (r)\right) \int _0^r \cosh ^2\left( \xi _\alpha (s) \right) f(x_0(s)) {\text {d}}s {{\mathrm{d}}}r. \end{aligned}$$
(12b)

2.5 Results and comparison to numerical solutions

We consider four sample course profiles:

$$\begin{aligned} \begin{array}{ll} \theta _1(x) &{}= \frac{3x}{100(x+3)}, \qquad \theta _2(x) = \frac{-3x}{100(x+3)}, \\ \theta _3(x) &{}= -\frac{\sin (30x)}{50}, \qquad \,\theta _4(x) = -\frac{\sin (2x)}{50}. \end{array} \end{aligned}$$
(13)

The corresponding course height profiles are given by

$$\begin{aligned} h=\int _0^ x \sin \theta (s)\,{\text {d}}s, \end{aligned}$$
(14)

and are illustrated in Fig. 2a.

We take the system parameters to be values we would typically expect in a race [1, 3, 16],

$$\begin{aligned}&\hat{M} = 80 \,{\text {kg}},&\hat{F}_{\text {p}} = 25 \,{\text {N}}, \quad&\hat{F}_{\text {f}} = 3 \,{\text {N}}, \\&\hat{\rho } = 1.3\, {\text {kg}}/{\text {m}}^{3},&c_{\text {D}} = 0.8, \quad&\hat{A} = 0.3 \,{\text {m}}^{2}, \end{aligned}$$

and assume that the solo rider has the same mass as the mean, \(\hat{M}\). This gives the dimensionless parameters and scaling factors to be \(m=1\), \(F_0\approx 0.028\), \(\hat{L}\approx 510\)m, and \(\hat{T}\approx 7.2\)s. We also take the initial velocity to be \(v_i=0.16\) (corresponding to about 40km/h or 11m/s, a typical cycling speed). We choose \(\alpha\) by taking the average of \(\theta\) over the domain, giving the values displayed in Table 1.

Table 1 Course profiles given by (13) and used in Fig. 2
Full size table
Fig. 2
figure 2

a Model course profiles as given in (13). The height, h, is given by (14). b Numerical solutions for velocity and c numerical solutions for distance travelled for course profiles as given in (13) and shown in a. The asymptotic solutions are illustrated by the dashed lines, showing excellent agreement for courses \(\theta _1\), \(\theta _2\) and \(\theta _3\). The agreement for \(\theta _4\) is not so close due to the large variations in \(\theta _4\) for which the assumptions of the asymptotic analysis breaks down. The agreement can be improved by dividing the course into smaller sections in which the angle deviates less from the mean. d Time taken to complete a course of length X with profiles as given in (13). The asymptotic predictions given by (15) are shown by the dashed lines

Full size image

The function ode45 in MATLAB is used to solve the full system (5) numerically without making any approximations on the course gradient. This can be used to check that the asymptotic solution derived in Sect. 2.4 is close to the actual solution by plotting solutions for the choices of \(\theta\) given above. The asymptotic solutions are compared with the numerical solutions to the full system and shown in Fig. 2b, c.

For smooth inclines and declines (\(\theta _1\) and \(\theta _2\)) the asymptotic approximation captures the behaviour well. The rapidly oscillating function \(\theta _3\) in (13) corresponds to a road that has many small hills and the asymptotic prediction also provides a good approximation, even though \(\theta\) is never close to being constant. This suggests that the asymptotic solution should be a good approximation if there are small undulations in the course. We do, however, see that issues can arise when the variations become too large, as seen for \(\theta _4\), and cumulative errors can arise. However, as discussed earlier, we are able to accommodate courses like this by separating them into sections of almost constant slope and approximating with different \(\alpha\) for each segment.

2.6 Time to complete a course

We wish to find the time taken, \(T_{\text {end}}\), to travel the total course distance X. To do this we can use a series expansion, writing \({T_{\text {end}} = T_0 + \varepsilon T_1 + O(\varepsilon ^2)}\), to see

$$\begin{aligned} X = x(T_{\text {end}}) = x_0(T_0) + \varepsilon \big [ T_1\dot{x}_0(T_0) + x_1(T_0) \big ] + O(\varepsilon ^2), \end{aligned}$$

where we recall that \(x_0\) and \(x_1\) are known functions given by (11b) and (12b). Equating orders of \(\varepsilon\) gives

$$\begin{aligned} x_0(T_0) = X, \quad T_1 = \frac{-x_1(T_0)}{\dot{x}_0(T_0)}. \end{aligned}$$

We are able to invert \(x_0(T_0)\) and thus obtain the complete explicit solution up to \(O(\varepsilon )\),

$$\begin{aligned} T_0(X)&= \frac{m}{\sqrt{F_\alpha }}\left[ {{\mathrm{arcosh}}}\exp \left( \frac{X - \sigma _\alpha }{m} \right) - \tau _\alpha \right] , \end{aligned}$$
(15a)
$$\begin{aligned} T_1(T_0)&= \frac{\cos \alpha \displaystyle \int _0^{T_0} \left[ {{\mathrm{sech}}}^2\xi _\alpha (r) \int _0^{r} \cosh ^2\xi _\alpha (s) f(x_0(s)) {\text {d}}s \right] {\text {d}}r}{\sqrt{F_\alpha }\tanh \xi _\alpha (T_0)}, \end{aligned}$$
(15b)

where \(\tau _\alpha ={\text {artanh}}{\sqrt{F_\alpha }/v_i}\).

Again we use MATLAB to obtain numerical solutions as shown in Fig. 2d, and find good agreement with the asymptotic solution (15), with slight discrepancies arising for course \(\theta _4\) in the same way as seen in Fig. 2b, c.

Now that we have confidence in our asymptotic solutions we will use these results to compare the course completion time for a breakaway rider and the main field of riders. The explicit nature of the asymptotic solutions enable us to perform efficient parameter sweeps.

3 Modelling a group of riders and a breakaway

We now use the equations found in the previous section to seek an optimal strategy for a rider to break away from the main field of riders and finish in the shortest possible time. For simplicity we restrict our attention to the case of a single breakaway rider, who loses the benefit of drag reduction from being in the peloton. However, we note that the methods we use readily generalize for a small group of breakaway riders who benefit from drag reduction themselves.

We consider a course of length X and find the time it takes the main field to complete the course, \(T_\text {end}\). We then suppose a breakaway rider travels with the peloton up to some distance along the course, \(X_{\text {b}}\), before breaking away and travelling alone until the end of the course. Using this formulation we will find the time for the breakaway rider to complete the course, \({T}_{{\text {b}},\text {end}}\). We will seek the maximum difference in completion times, \(\Delta T_\text {end}=T_\text {end}-{T}_{{\text {b}},\text {end}}\), by varying the breakaway position, \(X_{\text {b}}\).

3.1 Governing equations

We model the main field by considering the average of each of the forces that act on the riders under the drag reduction. It is shown in the work of Kyle [8] that a rider cycling directly behind another rider experiences a drag reduction of approximately one third. We thus take the drag multiplication factor for the peloton, \(\gamma =0.7\) but acknowledge that adjustments in this factor to capture any particular race scenario may be implemented in an identical manner. We suppose that the pedal force, \(F_{\text {p}}\), exerted in the peloton is equal to the sustainable force, \(F_{\text {s}}\), as chosen for the single rider in Sect. 2. This choice corresponds to the peloton applying the maximum constant force that can be exerted for the entire duration of the race without suffering fatigue effects. Although in races we see that riders in the slipstream may not pedal continuously, we model the pedal force to be constant as a reasonable simplifying assumption. This yields a modification of (5) to capture the motion of the peloton:

$$\begin{aligned} \ddot{x} = F_0 - \gamma \dot{x}^2 - \sin \theta (x), \end{aligned}$$
(16)

where the mass factor \(m=1\), as the mass is scaled by the average mass of the riders in the peloton. We assume that m remains at this value for the peloton when a rider breaks away, which is a good approximation for a large number of riders in the peloton or if the breakaway rider’s mass is close to that of the average of all the riders.

Breakaway riders lose the benefit of slipstreaming, but escape from the peloton by providing a higher pedal force, which may depend on time, say \(F_{\text {b}}=F_{\text {b}}(t)\), so that the breakaway rider exerts a total pedal force \(F_{\text {p}}=F_{\text {s}}+F_{\text {b}}\). For the breakaway riders we model the displacement from the breakaway position, \(x_{\text {b}}(t_{\text {b}})\), with \(x_{\text {b}}(0)=0\), where \(t=t_{\text {b}}+T_{\text {b}}\) and \(T_{\text {b}}\) is the time of the breakaway, that is, \(x(T_{\text {b}})=X_{\text {b}}\). Then, for a single breakaway rider we have

$$\begin{aligned} m_{\text {b}}\ddot{x}_{\text {b}} = F_0 + F_{\text {b}} - \dot{x}_{\text {b}}^2 - m_{\text {b}}\sin {\theta }_{\text {b}}(x_{\text {b}}), \end{aligned}$$
(17)

where \({\theta }_{\text {b}}(x_{\text {b}})=\theta (x_{\text {b}}-X_{\text {b}})\).

By asserting that \(\ddot{x}_{\text {b}}>\ddot{x}\) at a breakaway point \(x=X_{\text {b}}\), where \(\dot{x}_{\text {b}}=\dot{x}\), we can use (16) and (17) to find the initial extra force a rider will need to provide to accelerate away from the peloton:

$$\begin{aligned} F_{\text {b}}(0)> (1 - m_{\text {b}}\gamma )\dot{x}^2 + F_0(m_{\text {b}} - 1). \end{aligned}$$
(18)

We see from (18) that a lower breakaway force is thus needed if the velocity is lower when breaking away (for example, if the riders are cycling uphill), provided \(m_{\text {b}}<1/\gamma \approx 1.4\), which is consistent with the fact that breakaways predominantly happen on hill stages and are attempted by lighter riders. As a benchmark we consider a flat course, with the peloton riding at constant velocity \(\dot{x}=\sqrt{F_0/\gamma }\). Then, with \(m_{\text {b}}=1\), \(\gamma =0.7\), and \(F_0=0.028\), we find a breakaway rider will need to increase their pedal force by at least 37.5% to break away, from \(F_{\text {s}}=0.032\) to at least \(F_{\text {s}}+F_{\text {b}}(0)=0.044\). Although this is a significant increase, it is important to note that \(F_{\text {s}}\) is the average force provided by riders in the main field, which is likely to be significantly below their maximum.

In this section we assume the extra pedal force to be a constant, that is we set \(F_{\text {b}}=F_{\textrm{b}0}\). We will relax this assumption in Sect. 5, but for now we will find that this allows us to model the situation analytically using the solutions found in Sect. 2 and gives an explicit understanding of the parametric dependence of the system. We will also assume for simplicity that the main field of riders do not react to the breakaway in terms of altering their pedal force.

3.2 Model solutions for a constant breakaway force

We now solve (16) in an identical manner to the analysis in Sect. 2.4 for a weakly undulating course. The resulting expressions for the leading- and first-order solutions for the position and velocity are given by (11) and (12) respectively, with \(F_\alpha\) replaced by \(F_\alpha /\gamma\) and m replaced with \(1/\gamma\). The time taken to reach a point X in the course is obtained from (15) with the same replacements, that is,

$$\begin{aligned} T_0(X)&= \frac{1}{\sqrt{\gamma F_\alpha }}\bigg [ {{\mathrm{arcosh}}}\exp \big ( \gamma (X-\sigma _\gamma ) \big ) - \tau _\gamma \bigg ], \end{aligned}$$
(19)
$$\begin{aligned} T_1(T_0)&= \frac{\sqrt{\gamma }\cos \alpha }{\sqrt{F_\alpha }\tanh \xi _\gamma (T_0)} \int _0^{T_0} \bigg [ {{\mathrm{sech}}}^2\xi _\gamma (r) \\&\quad \times \int _0^{r} \cosh ^2\xi _\gamma (s) f(x_0(s)) {\text {d}}s \bigg ] {\text {d}}r, \end{aligned}$$
(20)

where

$$\begin{aligned} F_\alpha&=F_0-\sin \alpha , \quad \tau _\gamma ={{\mathrm{artanh}}}\left( \sqrt{\gamma }v_i/\sqrt{F_\alpha }\right) , \\ \xi _\gamma (t)&=\sqrt{\gamma F_\alpha } t + \tau _\gamma , \quad \text {and}\quad \sigma _\gamma =\log \left| {\gamma v_i^2}/{F_\alpha } - 1\right| /2\gamma . \end{aligned}$$

We now suppose the rider breaks away with a constant breakaway force \(F_{\text {b}}=F_{\textrm{b}0}\) at time \(t=T_{\text {b}}\) and position \(x(T_{\text {b}})=X_{\text {b}}\), at which point the velocity is given by \(\dot{x}(T_{\text {b}})\), found from the equations resulting from the above procedure. We again follow a similar process, this time replacing \(F_\alpha\) with \(F_\alpha +F_{\textrm{b}0}\) and m with \(m_{\text {b}}\) in the analysis performed in Sect. 2.4, and use \(\dot{x}_{\text {b}}(0)=\dot{x}(T_{\text {b}})\), which allows us to obtain solutions for \(\dot{x}_{\text {b}}(t_{\text {b}})\) and \(x_{\text {b}}(t_{\text {b}})\).

Our interest lies, however, in the solution for the completion time. To extract this, we reverse the time transformation \(t=t_{\text {b}}+T_{\text {b}}\) and use the solutions (19) and (20) for \(T_{\text {b}}\), to give

$$\begin{aligned} {T}_{\textrm{b},\text {end}}(X; X_{\text {b}})&= T_0(X_{\text {b}}) + {T}_{0,\textrm{b}}(X-X_{\text {b}}) \nonumber \\& \quad +\varepsilon \bigg [ T_{1}\big ( T_0(X_{\text {b}}) \big ) + {T}_{1,\textrm{b}}\big ( {T}_{0,\textrm{b}}(X-X_{\text {b}}) \big ) \bigg ], \end{aligned}$$
(21)

with

$$\begin{aligned} {T}_{0,\textrm{b}}(X_{\text {b}})&= \frac{m_{\text {b}}}{\sqrt{F_\alpha +F_{\textrm{b}0} }}\left[ {{\mathrm{arcosh}}}\exp \left( \frac{X_{\text {b}} - \sigma _{\text {b}}}{m_{\text {b}}} \right) - \tau _{\text {b}} \right] , \end{aligned}$$
(22)
$$\begin{aligned} {T}_{1,\textrm{b}}({T}_{0,\textrm{b}})&= \frac{\cos \alpha }{ \sqrt{F_\alpha +F_{\textrm{b}0} }\tanh \xi _{\text {b}}({T}_{0,\textrm{b}})} \int _0^{ {T}_{0,\textrm{b}} } \bigg [ {{\mathrm{sech}}}^2\xi _{\text {b}}(r)\nonumber \\& \quad \times \int _0^{r} \cosh ^2\xi _{\text {b}}(s) F_{\textrm{b}0}({x_{\text {b}}}_0(s)) {\text {d}}s \bigg ] {\text {d}}r, \end{aligned}$$
(23a)

where

$$\begin{aligned} \tau _{\text {b}}&={{\mathrm{artanh}}}\left( \dot{x}_{\text {b}}(0)/\sqrt{F_\alpha +F_{\textrm{b}0}}\right) ,\\ \xi _{\textrm{b}}(t)&= \sqrt{F_\alpha +F_{\textrm{b}0}}t/{m_{\text {b}}}+\tau _{\text {b}},\\ \text {and}\quad \sigma _{\textrm{b}}&={m_{\text {b}}}/{2}\log \left| {\dot{x}_{\text {b}}(0)^2}/(F_\alpha +F_{\textrm{b}0}) - 1 \right| . \end{aligned}$$

We then have the time difference between the breakaway rider and the peloton completing the course, \(\Delta T_\text {end}=T_\text {end}-{T}_{\textrm{b},\text {end}}\), given by (19), (20) and (21). Finally, we can use this result to compute the optimal breakaway position \(X_{\text {b}}\), which maximizes the time difference between the breakaway rider and the peloton.

3.3 Results

For a flat course with a constant breakaway force that is sufficient to leave the peloton, the strategy that maximizes the time that a rider finishes ahead of the peloton is trivial, with the rider recommended to break away as soon as possible. However, for an undulating course, an optimum breakaway position emerges (Fig.3). Specifically, this suggests that a steep hill close to the end provides a good place to break away, as we would expect considering the lower velocity when riding against gravity and thus reduced penalty in increased drag for breaking away. The larger the hill height, the greater the gains that can be made. We also find that the potential gains increase slowly as the breakaway position is delayed until further up the hill, but upon reaching the optimal breakaway position, in this case around halfway up the hill, the gains subsequently drop off much more rapidly. This suggests that, in a real race whose final course profile comprises an uphill followed by a downhill section, if a cyclist does not suffer from fatigue effects and is able to provide a constant breakaway force then it is better to break slightly sooner rather than too late.

Fig. 3
figure 3

Time taken for breakaway rider to complete a course compared to the peloton, for a course profile given by \(h=h_0{\text {exp}}(-\beta (x-x_\text {max})^2)\) (shown schematically in inset), with \(h_0=0.02,0.025,0.03,0.035,0.04\), \(\beta =0.5\) and \(x_\text {max}=6\). Here, \(m_{\text {b}}=1\), \(F_0=0.028\) and \(F_{\textrm{b}0}=0.011\). We choose \(v_i=\sqrt{F_0/\gamma }=0.2\) to give \(\ddot{x}(0)=0\), so that the peloton is travelling at a constant speed

Full size image

4 Fatigue effects when attempting a breakaway

In the previous section we assumed the breakaway force was constant to allow us to solve the system using asymptotic methods. In this section, we seek an improved model for how the force provided by a breakaway rider might vary.

4.1 Cause of the fatigue

As seen in Sect. 3.1, for a rider to break away from the peloton the excess force they apply, \(F_{\text {b}}\), must be high enough to counter the increase in drag experienced by a solo rider (Eq. 18). As a consequence of applying this excess force, fatigue effects will come into play, resulting in the force that the rider is actually able to exert subsequently dropping back towards the sustainable force of the peloton (or possibly even below for a short period of time while the rider recovers, as we will discuss later on). We expect the fatigue to play a role both on a short timescale, due to anaerobic respiration, preventing sustained bursts of speed, and on a longer time, due to depletion of energy reserves.

The short-term fatigue effect is commonly attributed to lactic acid build-up as a consequence of anaerobic respiration. However, another cause of fatigue is the net movement of potassium ions (K\(^+\)) out of contracting skeletal muscle [12]. There are contrasting opinions on whether lactic acid or potassium has the larger effect on force output, as noted by Hargreaves [4]: “Generally, the lactate ion does not appear to have any major negative effects on the ability of skeletal muscle to generate force, although conflicting data exist in the literature. Of greater consequence is...the movement of strong ions (e.g., K\(^+\)) across the muscle cell membrane.” Here we choose to model the movement of potassium ions, but note that a similar mathematical relationship would apply if we were considering lactic acid and so this assumption will not affect our conclusions. In the following sections we incorporate the effect of fatigue due to anaerobic respiration and depletion of energy reserves.

4.2 Potassium transport model

We denote the (dimensionless) measure of increase in concentration of extracellular potassium ions as p. The concentration of potassium ions in the blood increases linearly with oxygen uptake (VO\(_2\)) up to the maximum sustainable uptake (100%), where VO\(_2\) is attributed the description ‘exercise intensity’  [12]. We assume that applying a pedal force higher than the sustainable force, \(F_{\text {s}}\), will result in an increase in p. We assume a linear relationship, which gives us the equation

$$\begin{aligned} \frac{{{\mathrm{d}}}p}{{{\mathrm{d}}}t} = F_{\text {p}} - F_{\text {s}}. \end{aligned}$$
(23b)

We note that a constant of proportionality would be required on the right-hand side of (24) if p were to correspond to the actual concentration of extracellular potassium. However, here we are interested only in a measure of the excess concentration so this constant may be incorporated into our definition of p. Equation (24) predicts there will be a net movement of potassium ions back into the muscle cells when \(F_{\text {b}}<0\), thus allowing for recovery by applying a lower force than that of the peloton. The actual output force will decrease as potassium ions move out of the muscle cells, as confirmed by Cairns [2] and McKenna [14]. This force decreases when the ion concentration exceeds 8 mM [2, 14, 17]. Beyond this value it is reasonable to model the actual output force \(F_{\text {p}}\) to decrease exponentially with p.

The work of Cairns [2] and McKenna [14] also shows that when relating the force exerted to the potassium concentration we should consider adding in a threshold. Sejersted [17] notes that there is not a simple linear relationship between the potassium concentration and force development: indeed, moderate increases in concentration may even cause force potentiation, but at high concentrations (i.e., higher than 8–10 mM), force development is suppressed. To incorporate this behaviour into our model we introduce a threshold potassium concentration, \(p_1\), below which we assume the output force is unaffected by the value of p. We thus assume the breakaway force is governed by

$$\begin{aligned} F_{\text {p}} = \left\{ \begin{array}{ll} \ F_{\text {s}} + F_{\textrm{b}0} &{}\quad \text {for } p\le p_1\\ \left( F_{\text {s}} + F_{\textrm{b}0} \right) {\text {e}}^{-a(p-p_1)} &{}\quad \text {for } p>p_1, \end{array}\right. \end{aligned}$$
(24)

where \(a\ge 0\). When \(a=0\) we recover the case where the pedal force is unchanged when the threshold potassium concentration is crossed. The force \(F_{\text b0}\) is the additional force that a breakaway rider attempts to apply, in line with the analysis presented in Sect. 3.1. The potassium concentration increases less in trained athletes [12], which translates to a lower value for the parameter a for trained cyclists, meaning they can sustain a higher force for longer.

Substituting (25) into (24) and applying the initial condition \(p(0)=0\) gives

$$\begin{aligned} F_{\text {p}}(t) = \left\{ \begin{array}{ll} F_{\text {s}} + F_{\textrm{b}0} &\quad \text {for }t\le t_1\\ \frac{\displaystyle F_{\text {s}}(F_{\text {s}} + F_{\textrm{b}0})}{\displaystyle F_{\text {s}} + F_{\textrm{b}0}\left( 1 - {\text {e}}^{-aF_{\text {s}}(t-t_1)} \right) } &\quad \text {for } t>t_1, \end{array}\right. \end{aligned}$$
(25)
$$\begin{aligned} p = \left\{ \begin{array}{ll} F_{\textrm{b}0} t &\quad \text {for }t\le t_1\\ p_1 + \frac{1}{a}\log \left( 1 + \frac{F_{\textrm{b}0}}{F_{\text {s}}}\left( 1 - {\text {e}}^{-aF_{\text {s}}(t-t_1)} \right) \right) &\quad \text {for } t>t_1, \end{array}\right. \end{aligned}$$
(26)

where \(t_1=p_1/F_{\textrm{b}0}\). The results of this model are illustrated in Fig. 4.

Fig. 4
figure 4

a Total pedal force exerted by a breakaway rider, \(F_{\text {p}}\), and b the corresponding excess concentration of potassium ions, p, versus time, given respectively, by (26) and (27). Here, \(F_{\text {s}}=0.032\), \(F_{\textrm{b}0}=0.8F_{\text {s}}\), \(p_1=0.1\) and \(a=0.5,1,1.5,2\). The horizontal line in a shows the sustainable force, \(F_{\text {s}}\). The pedal force remains constant until the potassium concentration reaches the critical value, \(p_1\)

Full size image

4.3 Stamina model

After a rider breaks away we also expect there to be stamina limitations, which will decrease the force that can be exerted over a sustained time. As a consequence of the additional exertion the output force may dip below the sustainable force. We model this by replacing \(F_{\textrm{b}0}\) with a modified force \(F_{\textrm{bs}}\) that incorporates the reduction due to stamina (before applying the potassium limitation) so that (25) becomes

$$\begin{aligned} F_{\text {p}} = \left\{ \begin{array}{ll} F_{\text {s}} + F_{\textrm{bs}}(t) &\quad \text {for }p\le p_1\\ \left( F_{\text {s}} + F_{\textrm{bs}}(t) \right) {\text {e}}^{-a(p-p_1)} &\quad \text {for } p>p_1. \end{array}\right. \end{aligned}$$
(27)

We assume that \(F_{\text bs}\) is governed by the equation

$$\begin{aligned} \frac{{{\mathrm{d}}}F_{\textrm{bs}}}{{{\mathrm{d}}}t} = -b F_{\textrm{b}0} F_{\textrm{bs}}, \quad F_{\textrm{bs}}(0)=F_{\textrm{b}0}, \end{aligned}$$
(28)

where \(b \ge 0\), which gives the solution

$$\begin{aligned} F_{\textrm{bs}}(t) = F_{\textrm{b}0} {\text {e}}^{-bF_{\textrm{b}0}t}. \end{aligned}$$
(29)

When \(b=0\) we recover the case where stamina plays no part. We can again solve the potassium equation (24) to get p(t) by substituting for \(F_{\text {p}}\) using (28) and (30). The solution for p(t) can then be substituted back into (28) to give

$$\begin{aligned} F_{\text {p}}(t) = \left\{ \begin{array}{ll} \ F_{\text {s}} + F_{\textrm{b}0} {\text {e}}^{-bF_{\textrm{b}0}t} &{}\quad \text {for } t\le t_2\\ \frac{(\displaystyle aF_{\text {s}} - bF_{\textrm{b}0})\left( F_{\text {s}} + F_{\textrm{b}0}{\text {e}}^{-bF_{\textrm{b}0}(t-t_2)} \right) }{\displaystyle aF_{\text {s}} - bF_{\textrm{b}0} + aF_{\textrm{b}0}\left( {\text {e}}^{-bF_{\textrm{b}0}(t-t_2)} - {\text {e}}^{-aF_{\text {s}}(t-t_2)} \right) }, &{}\quad \text {for }t>t_2, \end{array}\right. \end{aligned}$$
(30)

where \(t_2=-\big (\log (1-bp_1)\big )/(bF_{\text {b}})\).

Fig. 5
figure 5

a Total pedal force exerted by a breakaway rider, \(F_{\text {p}}\), given by (31), and b the corresponding concentration of potassium ions, p, versus time, governed by potassium effects and stamina, found by solving (24), (28), and (30). Here, \(F_{\text {s}}=0.032\), \(F_{\textrm{b}0}=0.8F_{\text {s}}\), \(p_1=0.1\), \(a=0.5\) and \(b=0.5,1,1.5,2\). The horizontal line in a shows the sustainable force, \(F_{\text {s}}\)

Full size image

The stamina effects considered in this model lead to an initial slow decrease in pedal force before the deficit potassium in the muscle cells has a severe effect on the force output, resulting in a subsequent rapid drop (Fig. 5). As expected, the addition of the stamina limitation results in the force dropping below the sustainable force, \(F_{\text {s}}\), for a marked period of time, before the potassium level recovers towards the threshold value, \(p_1\). In reality we might expect a rider to recover after a while, meaning that if they were caught by the peloton they could break away a second time. However, we are only concerned with single breakaways, as our model predicts no advantage of breaking away twice.

5 Numerical solutions under fatigue effects

We now consider the implications of a breakaway force that varies with time due to stamina limitations. As in Sect. 2, we assume that the rider exerts the maximum additional force they can when breaking away, which is \(F_{\text {b}}=F_{\text {p}}-F_{\text {s}}\), where \(F_{\text {p}}\) for a breakaway rider is given by (31), so we have

$$\begin{aligned} {F}_{\text {b}}(t) = \left\{ \begin{array}{ll} F_{\textrm{b}0} {\text {e}}^{-bF_{\textrm{b}0}t} &\quad \text {for }t\le t_2\\ \frac{\displaystyle F_{\textrm{b}0}\left( aF_0{\text {e}}^{-aF_0(t-t_2)} - bF_{\textrm{b}0}{\text {e}}^{-bF_{\textrm{b}0}(t-t_2)} \right) }{\displaystyle aF_0 - bF_{\textrm{b}0} + aF_{\textrm{b}0}\left( {\text {e}}^{-bF_{\textrm{b}0}(t-t_2)} - {\text {e}}^{-aF_0(t-t_2)} \right) }, &\quad \text {for }t>t_2. \end{array}\right. \end{aligned}$$
(31)

We note that in the absence of stamina and fatigue limitations, \(a=b=0\), we have \(F_{\text {b}}=F_{\textrm{b}0}\), recovering the case studied in Sect. 3.1. As discussed earlier, the breakaway force, \(F_{\text {b}}\), has the potential to become negative, corresponding to overexertion of the rider so that they can no longer maintain the sustainable pedal force of the peloton, \(F_{\text {s}}\). This can typically occur in a cycle race where a breakaway rider is first caught by the peloton before being subsequently dropped.

We solve the equations for the peloton, (16), and the breakaway rider, (17), with \(F_{\text {b}}\) given by (32), numerically for different breakaway positions to determine the best position to break away. As we are only considering single breakaways, we only need to consider the final part of the race. For a flat course we find that, for the parameters considered here, the best breakaway point is around \(x=X-5.5\), which corresponds to 2.5km from the end of the race (see Fig. 6a). We note that this prediction is independent of the total length of the course (provided the course is sufficiently long that the start of the race has negligible effect). While the optimum value will depend on the physical parameters associated with the rider, the approach is the same: to have a velocity higher than the main field for as much time as possible, as demonstrated in Fig. 6b.

Fig. 6
figure 6

Motion along the last 20 length units (\(\approx 10\)km) of a flat course, given by (16), (17), and (32). Here, \(m_{\text {b}}=1\), \(F_{\text {s}}=0.032\), \(F_{\textrm{b}0}=0.8F_{\text {s}}\), \(p_1=0.1\), \(a=0.5\) and \(b=0.5\)

Full size image

We have already seen in Sect. 3 that the success depends on the breakaway force being sufficiently large compared to the sum of the gravitational and pedal forces of the main field, as given by Eq. (18). As for a constant breakaway force, the model predicts that it is best to break away when cycling uphill, when the velocity is lower, and thus the penalty due to the increased drag when cycling alone are minimized.

Fig. 7
figure 7

Effect of valley position on breakaway success. Motion along the last 20 length units (\(\approx 10\)km) of a valley course profile given by \(h=h_0\exp \bigl (-\beta (x-x_\text {min})^2\bigr )\) with \({\text {h}}_0=-\,0.04\), \(\beta =0.5\), \(m_{\text {b}}=1\), \({{\text {F}}}_{\text {s}}=0.032\), \(F_{\text{b0}}=0.8F_{\text {s}}\), \(p_1=0.1\), \(a=0.5\) and \(b=0.5\). The solution is given by (16), (17), and (32)

Full size image

We next study the effect of course contours, beginning with a course composed of a single valley. The optimal breakaway position depends strongly on the valley location as seen in Fig. 7. Figure 7b indicates that the best position to break away is generally just after the trough of the valley since the velocity of the main field of riders will be low as they travel uphill out of the valley, meaning they benefit less from the drag reduction. One exception to this is when the trough occurs very close to the end as seen in Fig. 7c, in which case breaking away earlier can result in a larger win margin to make the most of the extra force available. A second exception is when the valley occurs too far from the end of a race (for example \(x_\text {min}=6\) in Fig. 7a), where the advantage of breaking away in the valley is countered by the large subsequent time without slipstreaming, in which the breakaway rider has a velocity lower than that of the peloton. For valleys that occur very early on, the optimal breakaway position is \(x=X-5.5\), which is the same as for the flat course. When the trough roughly coincides with this position (\(x_\text {min}\approx 14.5\) in Fig. 7c, as seen with \(x_\text {min}=14\) in Fig. 7a) we obtain the best possible win margin of all courses.

Considering the same simulation for peaks instead of valleys yields a similar result (see Fig. 8), with the optimal breakaway position generally being before the peak, when the velocity is lower. We also notice that, despite the course now finishing with a downhill section where the velocity, and hence drag, is higher, the breakaway rider is able to finish a similar amount of time ahead of the peloton to when there is a valley with the same change in altitude and the course ends with an uphill stretch.

Fig. 8
figure 8

Effect of peak position on breakaway success. Motion along the last 20 length units (\(\approx 10\) km) of a hill course profile given by \(h=h_0\exp \bigl (-\beta (x-x_\text {max})^2\bigr )\) with \(h_0=0.04\), \(\beta =0.5\), \(x_\text {max}=6,10,14,18\), and \(m_{\text {b}}=1\), \(F_{\text {s}}=0.032\), \(F_{\textrm{b}0}=0.8F_{\text {s}}\), \(p_1=0.1\), \(a=0.5\) and \(b=0.5\). We choose \(v_i=0.2\) so that initially the peloton is moving at constant velocity on a flat course (given by (16) with \(\ddot{x}=0\)). The solution is given by (16), (17), and (32)

Full size image

Finally, we consider the effect of the hill height. We fix the position of the maximum and vary the height and gradient of the course separately to understand when the hill offers a good breakaway opportunity. We emphasize that there is no restriction on the gradient of the hill, and so this analysis holds for shallow gradients or extreme mountain stages.

The results shown in Fig. 9 indicate that a shallower hill lengthens the uphill section and the optimal breakaway position occurs at some point in this section, depending on the gradient. From Fig. 10 we see that even a short hill that occurs early in a race can provide a good place to break away early if it is high enough. The generic strategy in all of these cases is to break away over the period of low velocity, during the steep climb. It is here that the drag reduction experienced in the main field of riders is lower, and applying a higher force allows the breakaway rider to advance a significant distance ahead in this period, making it difficult for the peloton to catch up.

Fig. 9
figure 9

Effect of hill gradient on breakaway success. Motion along the last 20 length units (\(\approx 10\) km) of a hill course profile given by \(h=h_0\exp \bigl (-\beta (x-x_\text {max})^2\bigr )\) with \(h_0=0.04\), \(\beta =0.1,0.3,0.5,0.7\), \(x_{\text {max}}=12\), and \(m_{\text {b}}=1\), \(F_{\text {s}}=0.032\), \({{\text {F}}}_{\textrm{b}0}=0.8{{\text {F}}}_{{\text {s}}}\), \(p_1=0.1\), \(a=0.5\) and \(b=0.5\). We choose \(v_i=0.2\) so that initially the peloton is moving at constant velocity on a flat course (given by (16) with \(\ddot{x}=0\)). The solution is given by (16), (17), and (32)

Full size image
Fig. 10
figure 10

Effect of hill height on breakaway success. Motion along the last 20 length units (\(\approx 10\) km) of a hill course profile given by \(h=h_0\exp \big (-\beta (x-x_\text {max})^2\bigr )\) with \(h_0=0.02,0.03,0.04,0.05\), \(\beta =0.5\), \(x_{\text {max}}=12\), and \(m_{\text {b}}=1\), \(F_{\text {s}}=0.032\), \(F_{\textrm{b}0}=0.8F_{\text {s}}\), \(p_1=0.1\), \(a=0.5\) and \(b=0.5\). We choose \(v_i=0.2\) so that initially the peloton is moving at constant velocity on a flat course (given by (16) with \(\ddot{x}=0\)). The solution is given by (16), (17), and (32)

Full size image

6 Conclusions

In this paper we have formulated a model for the motion of a cyclist in a race, to determine the optimal time to break away from the peloton. Using an asymptotic expansion for small deviations in the gradient of the course allowed us to produce an explicit expression for the time to complete a given course.

Initially we modelled the breakaway rider with a constant pedal force (higher than the peloton), which allowed us to use explicit asymptotic expressions. From this we obtained an equation for the time difference between the breakaway rider and the main field in terms of the breakaway position, allowing us to determine the optimal position. By considering a single hill and varying its characteristics we showed that breaking away when travelling uphill is optimal since rider velocities will be lower and thus the drag reduction in the peloton will be less significant. This analytical model can be used to predict the optimal position to break away in a given race for a given individual and course profile.

We then extended the analytical model by including fatigue effects in the pedal force, no longer assuming the pedal force of a breakaway rider would remain constant. We considered the movement of potassium ions out of the muscle cells, linking the potassium concentration to the force output and including a stamina limitation, which led to an equation describing the decay of the pedal force over time after a breakaway. This model must be solved numerically, but the asymptotic approximations enable us to perform parameter sweeps for the breakaway position on different course profiles to determine how the breakaway strategy may be altered depending on the steepness, length and position of hills along a course. The analysis imposed no constraints on the gradient of the hills, and so the methodology would hold for any course profile, including mountain stages.

The strategy for riders should be to break away at a position that allows a velocity higher than the peloton for as much of the course as possible. We found that the optimal way to achieve this is to break away just before the velocity is expected to be low for a sustained period of time, such as at the beginning of a long hill climb. Uphill sections allow the breakaway rider to create distance between themselves and the main field as a result of the reduced benefit from the drag reduction in the peloton. We also observed that if a hill occurs too early in the course the peloton will have time to catch up with a rider who uses the hill to break away, but an early uphill section may still be the optimal place to break away if it is sufficiently steep or long. As well as choosing a breakaway position where a velocity higher than the peloton can be sustained, it is of course also important to minimize the duration and magnitude of a breakaway rider velocity that is lower than the main field, where the gap will be decreasing. As a consequence of this, if an uphill section is followed by a downhill section, or if the uphill section is quite long, it may be optimal to break away halfway up the hill so that the extra force can be sustained up to the top of the hill.

This paper provides a framework for performing efficient parameter sweeps that determine the optimal strategy for breaking away in a cycling race. The methodology readily generalizes to more complex scenarios, for example, incorporating rider fitness and strategies (of which plentiful data will be available to a cycling team), the possibility of two or more riders breaking away from the main field together, and the peloton’s response to a breakaway. It would be prudent to investigate the influence of other physical and physiological factors, such as diet, nutrition, and training, which all play a vital role in rider performance [7]. Finally, it would be interesting to combine these ideas with the field of rider tactics, such as a rider faking a breakaway to tempt a reaction from riders in the main field. This opens up the enticing possibility that the type of modelling presented here may be combined with concepts from the field of non-cooperative game theory (see, for example, [11]) to explore a wider class of winning strategies.