Abstract
The two-body system is of great interest and complexity. To study the evolution of the two-body system under the influence of torque, a new Sturm-Liouville equation 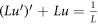 is derived from the Newtonian mechanism. Its solutions and the eigenvalue problem are investigated.
is derived from the Newtonian mechanism. Its solutions and the eigenvalue problem are investigated.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The two-body system has been studied extensively in physics, such as Kepler problem [1–3], Rutherford experiment [4, 5], Bohr model [6–8] and so forth. Based on the Newtonian mechanism, the trajectory of a particle in a two-body system is a conic section when angular momentum is a constant [9]. However, the evolution of the two-body system under the influence of torque is still improperly understood yet, which is of great interest and complexity. We introduce a new equation  derived from the Newtonian equation to extend the study of a two-body system under general circumstances. This equation turns out to be a Sturm-Liouville equation.
derived from the Newtonian equation to extend the study of a two-body system under general circumstances. This equation turns out to be a Sturm-Liouville equation.
Sturm-Liouville equations are ubiquitous and continuously growing in mathematical physics [10]. Many second-order differential equations arise from a variety of phenomena can ultimately be written as Sturm-Liouville type equations. Based on the Sturm-Liouville theory, their eigenvalues can be ordered and eigenvectors span an orthogonal basis [11, 12]. It has become the primary technique for us to gain insight into the spectra of a dynamical system [13, 14]. This paper will investigate the properties of the Sturm-Liouville equation on a two-body system via eigenvalue problem and its solutions.
2. Derivation of Sturm-Liouville equation of Two-body system
It begins with two fundamental equations on the two-body system equations (1) and (2). Equation (1) is Newton's law that the force between two bodies is proportional to the inverse square of the distance [7]. And equation (2) states the varying angular momentum caused by torque and mobility of angular momentum [9]. It is worthwhile noting that in this study, the angular momentum of the two-body system is not assumed to be a constant due to the influence of torque.
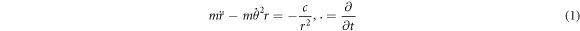
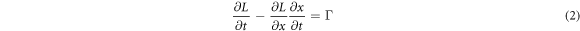
where, c is a constant; m is the particle's mass; r is the radius; θ is angular displacement; t is time; L is the orbital angular momentum; Γ is the torque.
Before the detailed analysis, let's simplify equation (1) into an ordinary differential equation. It is required to substitute r and 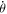 in equation (1) with r = 1/u and
in equation (1) with r = 1/u and 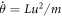 . That is [9]
. That is [9]
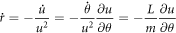
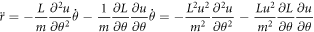

With the above calculation, equation (1) reads as the following second order differential equation with variable coefficients:
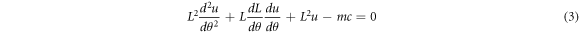
In this study, it will be assumed that there is a domain Θ in which L is analytic. By multiplying the factor 1/L to each term in equation (3), it can be written as a Sturm-Liouville equation.
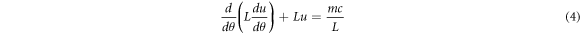
Without loss of generality, let all constants (m and c) in the equation to be 1. Then we have
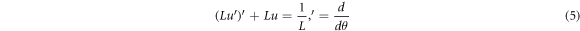
3. Solutions of equation (5) 
As a deterministic problem, equation (5) can be solved with given initial value conditions or boundary value conditions in principle. When angular momentum is a constant, the equation turns to be a Kepler problem. For an attentive reader, it is straightforward to check that conic sections and Bohr orbits are solutions. In this paper, however, we pay particular attention to solutions with regard to varying angular momentum.
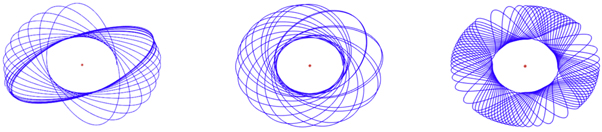
We can solve equation (5) subjected to some torque numerically. For instance, for a periodic torque  , the ode4 solver implemented by Runge-Kutta method in MATLAB [15] can sketch the trajectory of the particle in the two-body system given the initial value conditions. As shown in figure 1, under some circumstances, solutions
, the ode4 solver implemented by Runge-Kutta method in MATLAB [15] can sketch the trajectory of the particle in the two-body system given the initial value conditions. As shown in figure 1, under some circumstances, solutions 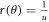 may look like a rotating elliptical orbit (leftmost and mid plots in figure 1) or a vibrating string (rightmost plot in figure 1).
may look like a rotating elliptical orbit (leftmost and mid plots in figure 1) or a vibrating string (rightmost plot in figure 1).
Figure 1. Numerical solutions of r(θ) solved by Runge-Kutta method portrait the trajectories of a particle in a two-body system if there is some torque. It observes that the particle is oscillating between an outer circle and an inner circle.
Download figure:
Standard image High-resolution imageFor nonhomogeneous equation (5), the analytical solution constitutes two components that particular solution and homogeneous solution.
For particular solution, suppose L has the form  and particular solution of u has the form
and particular solution of u has the form  . After plugging in L and u back to equation (5), we get
. After plugging in L and u back to equation (5), we get
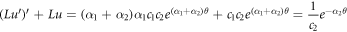
By matching coefficients and exponential power of both sides, then there is

Thus, as long as parameters c1, 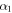 , c2 and α2 satisfy the following requirements, then
, c2 and α2 satisfy the following requirements, then 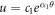 is a particular solution of equation (5) with regard to
is a particular solution of equation (5) with regard to  .
.

For the homogeneous solution which satisfies the equation 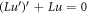 , we have
, we have
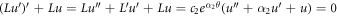
Hence,
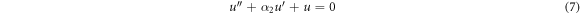
The homogeneous solution of u with regard to 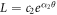 is
is

In combination with the particular solution of u, solution u with regard to 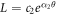 reads
reads

where parameters c1, α1, c2 and α2 satisfy the system of equation (6).
When α1 is a real number, logarithm spiral could be solutions of equation (5). By changing the sign of α1, it switch an inward logarithm spiral with an outward logarithm spiral. For instance 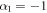 ,
,  is logarithm spiral solution with increasing angular momentum
is logarithm spiral solution with increasing angular momentum 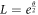 . And if α1 = 1,
. And if α1 = 1,  is the logarithm spiral with decreasing angular momentum
is the logarithm spiral with decreasing angular momentum  .
.
When α1 is a complex number, for instance 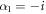 ,
,  and
and  satisfies equation (5). There is a great potential success for these solutions, however, also a challenge to interpret their physical meaning.
satisfies equation (5). There is a great potential success for these solutions, however, also a challenge to interpret their physical meaning.
4. Eigenvalue equation of two-body system
If we write equation (5) as an eigenvalue equation of a Sturm-Liouville operator T, such that  , it requests to introduce an additional equation
, it requests to introduce an additional equation  such that
such that

where the λ is spectral parameter, and the ω(θ) is weight function. The set of eigenvalue λ is the spectrum of the two-body system. Cautiously, as a side effect, the introduction of an additional equation may narrow down the solutions set.
Considering their physical meaning, u and L are not independent of each other. Different from most Sturm-Liouville equations in which eigenvectors share the same variable coefficients and weight function, solutions of the system of equation (8) have their own distinct variable coefficients and weight functions. If we plug in the solutions u and L back to the system of equation (8), this construction of solutions would help us investigate the eigenvalue and weight function of the equation.

Then, the most reasonable pair of eigenvalue and weight function in the system of equation (8) are
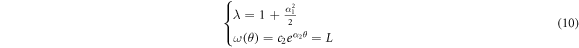
With the auxiliary equation 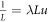 , we can rewrite the system of equation (8) with eigenvalue λ and weight function ω(θ) = L,
, we can rewrite the system of equation (8) with eigenvalue λ and weight function ω(θ) = L,
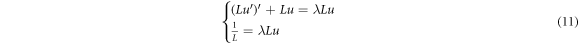
Then  and substitute L with
and substitute L with  ,
,
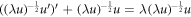
With the replacement 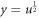 , we obtain
, we obtain
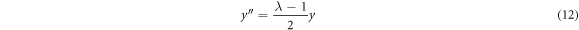
Solving the equation we get
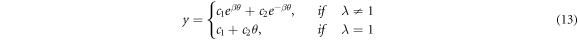
where 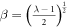 . Thus,
. Thus,
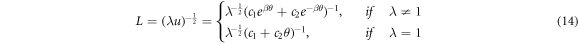
And,
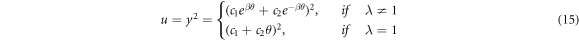
5. Conclusion
This paper presents a Sturm-Liouville equation  that calculates the two-body system under the influence of torque. The investigation of its solutions and eigenvalue problem shed light on the behavior and spectra of the two-body system.
that calculates the two-body system under the influence of torque. The investigation of its solutions and eigenvalue problem shed light on the behavior and spectra of the two-body system.
Acknowledgments
I would like to thank all anonymous referees' comments, suggestions, and efforts for the work. The discussion with referees significantly improved the quality and readability of the paper. Thank editor, associate editor and editorial assistants for smooth and efficient communication and coordination.