The first stars in the Universe

Abstract

1 Introduction

The formation of the first stars, in a universe that had not yet suffered chemical or magnetic stellar feedback, is a well-defined problem for theorists (Barkana & Loeb 2001). The advent of large telescopes has accelerated the observational quest for the first objects as astronomers have detected the light emitted by increasingly distant galaxies (Fan et al. 2003). A theoretical understanding of the first stars is of great importance as observations approach the pristine regime of the early Universe.

Stars are understood to form at high redshift out of gas that cooled and subsequently condensed to high densities in the cores of dark matter haloes. Because metals are absent in the pre-stellar Universe, the earliest available coolant is molecular hydrogen (H₂), and thus the minimum halo mass that can form a star is set by requiring the infalling gas to reach a temperature ≳1000 K required for exciting the rotational and vibrational states of H₂ (Tegmark et al. 1997). This has been confirmed with high-resolution numerical simulations containing gravity, hydrodynamics and chemical processes in the primordial gas (Abel, Bryan & Norman 2002; Bromm, Coppie & Larson 2002). These simulations showed that the first star formed within a halo containing ∼10⁵ M_⊙ in total mass; however, as we show, they could not estimate when the first star formed.

2 Limitations Of Simulations

In the real universe, the cosmological redshift z of each source implies a corresponding cosmic age at which the source is seen. Thus, the observable Universe can be divided into thin spherical shells around us, each containing a portion of the Universe that is observed at a given redshift z and is seen at the corresponding age. Galaxy formation in different shells is correlated due to density fluctuations on various scales. A simulation that wishes to determine when various objects are observed to form must encompass a sufficient portion of our past light cone.

Even with adaptive grid codes, full simulations are limited by current technology to tiny regions and only form a first star below redshift 20 (Abel et al. 2002) or 33 for the most recent simulations (OŚhea & Norman 2006). Even when great sacrifices are made regarding the accuracy of the physics involved, so that hydrodynamics and chemical evolution are neglected and the collapse of a star is only partially resolved, simulations still cannot capture the proper cosmological context. A direct simulation of the Universe out to the spherical shell at redshift 70 would require a simulated box of length 25 000 Mpc on a side [measured in comoving distance, which equals physical distance multiplied by a factor of (1 +z)]. The need to resolve each 10⁵ M_⊙ halo into 500 particles [required to determine the halo's evolution even crudely (Springel & Hernquist 2003)] determines the mass of each simulated particle, while the mean cosmic density of 4 × 10¹⁰ M_⊙ Mpc⁻³ yields the total mass of the simulated box, and implies a required total of 3 × 10²¹ particles. The maximum number achieved thus far is only ∼10¹⁰ (Springel et al. 2005). Early times have been probed by resimulating regions from a large initial simulation (Reed et al. 2005), forming star-forming haloes at z= 47 (the earliest to date), but with cosmological parameters for which the first galaxy actually formed at z∼ 82 according to our model below. Thus, the actual starting redshift of the era of galaxy formation can currently only be predicted analytically. For similar parameters, Miralda-Escudé (2003) made a rough analytical estimate [using the Press & Schechter (1974) halo mass function] and found that the first star formed at z∼ 48. A rough estimate by Wise & Abel (2005) found z∼ 71 using the improved Sheth & Tormen (1999) mass function (see also Section 3).

Simulations of the first stars also face a difficulty in the way their initial conditions are determined. Recent observations of the cosmic microwave background (CMB; Spergel et al. 2006) have confirmed the notion that the present large-scale structure in the Universe, as well as the galaxies within it, originated from small-amplitude density fluctuations at early cosmic times. Simulations thus assume Gaussian random initial fluctuations as might be generated by a period of cosmic inflation in the early Universe. The evolution of these fluctuations can be calculated exactly as long as they are small, with the linearized Einstein–Boltzmann equations. The need to begin when fluctuations are still linear forces numerical simulations of the first star-forming haloes to start at a high redshift, the highest to date being 600 (Reed et al. 2005). Current simulations neglect the contribution of the radiation to the expansion of the Universe and assume the Newtonian limit of general relativity which is valid in simulation boxes that are small with respect to the horizon. However, for a halo that forms around redshift 65, we find below that the corresponding region already must have had a moderately non-linear overdensity of δ∼ 20 per cent at z= 600 (δ is the density perturbation divided by the cosmic mean density). Indeed, we find that for initial conditions that ensure 1 per cent accuracy in δ, simulations must start deep in the radiation-dominated era, at z > 10⁶. Furthermore, we show that a small error in δ leads to a much larger error in the abundance of haloes at each redshift. The non-linearity of the initial conditions represents a previously unrecognized fundamental limitation of current methods of simulating the formation of the first star-forming haloes.

3 Spherical Collapse

While numerical simulations cannot determine the formation time of the first observable star, galaxy and halo formation can also be understood and described with a standard analytical model that has been quantitatively checked with simulations where the latter are reliable. The standard analytical model for the abundance of haloes (Press & Schechter 1974; Bond et al. 1991) considers the linear density fluctuations at some early, initial time, and attempts to predict the number of haloes that will form at some later time corresponding to a redshift z. First, the fluctuations are evolved to the redshift z using the equations of linear fluctuations, i.e. they are artificially linearly extrapolated even if they may become non-linear in some regions. The average density is then computed in spheres of various sizes. Whenever the overdensity in a sphere containing mass M rises above a critical threshold δ_c(M, z), the corresponding region is assumed to have collapsed by redshift z, forming a halo of at least mass M. Thus, the model separates the linear growth of fluctuations, which we calculate with standard codes (Seljak & Zaldarriaga 1996; Naoz & Barkana 2005; Yamamoto, Sugiyama & Sato 1998), from the non-linear collapse of objects, which determines the effective linear threshold δ_c(M, z).

Within this model, the non-linear collapse of a halo is analyzed by considering a uniform, spherically symmetric fluctuation whose collapse can be calculated by numerically solving ordinary differential equations; δ_c(M, z) is then determined as the value of the linearly extrapolated δ of the spherical region at the moment when the actual, non-linear δ diverges (i.e. the region collapses to a point). The classical calculation of spherical collapse in an Einstein–de Sitter (EdS) universe (i.e. a flat matter-dominated universe) yields δ_c= 1.686, a value that is independent of the halo mass and the collapse redshift (Gunn & Gott 1972). Given the power spectrum of the initial fluctuations, together with their linear growth, we can determine the chance that regions containing various initial masses M will reach the threshold δ_c at some final redshift z, and this forms the basis for estimating the abundance of haloes of mass M that form at a specific z (Press & Schechter 1974; Bond et al. 1991). We use the recently modified form of this model [Sheth & Tormen (1999), with the updated parameters suggested by Sheth & Tormen (2002)], which fits halo abundances in numerical simulations very accurately in regimes that include M= 10¹¹–10¹⁵ M_⊙ haloes at z= 0–10 (Jenkins et al. 2001; Springel et al. 2005) and M= 10⁶ M_⊙ haloes at z= 15–30 (Barkana & Loeb 2004; Yoshida et al. 2003). We note that other suggested mass functions (e.g. Reed et al. 2006) are in agreement with the Sheth & Tormen (1999) mass function if the updated parameters are used. Based on the plausible physical arguments behind this model, together with its quantitative success out to redshift 30, we extrapolate it to predict halo abundances at still-higher redshifts.

Our results assume cosmological parameters matching the latest CMB and weak lensing observations (Spergel et al. 2006). For the contributions to the energy density, we assume ratios relative to the critical density of Ω_m= 0.299, Ω_Λ= 0.701, and Ω_b= 0.0478, for matter, cosmological constant and baryons, respectively. We also assume a Hubble constant H₀= 100 h km s⁻¹ Mpc⁻¹ with h= 0.687, and a primordial power-law power spectrum with spectral index n= 0.953 and σ₈= 0.826, where σ₈ is the root-mean-square amplitude of mass fluctuations in spheres of radius 8 h⁻¹ Mpc.

Within this analytical model, we can account for early cosmic history when predicting the abundance of high-redshift stars and galaxies. We first calculate the correct value of δ_c(M, z) with a spherical collapse calculation that includes the full formation history of each halo (Fig. 1), starting out with a small perturbation and following its gravitational evolution until it collapses. We begin our calculation at a very high redshift when δ≪ 1, which implies that the overdense region containing the mass M is larger than the horizon. In this regime we use the cosmological Friedmann equations of general relativity, applied to the overdense region that we are following. We begin in the radiation-dominated era, and include throughout the contribution of the radiation to the cosmic expansion. Once the fluctuation enters the horizon, the overdense dark matter continues to collapse due to gravity, but the radiation pressure suppresses the sub-horizon perturbation in the photon density, and the coupling of the baryons to the photons (via Compton scattering) keeps the baryon perturbation small as well. Thus, in this regime we neglect the perturbation in the radiation and baryons and continue to evolve the spherical collapse of the dark matter perturbation. The formation of hydrogen at cosmic recombination (z∼ 1200) decouples the cosmic gas from its mechanical drag on the CMB, and the baryons (which constitute a significant 17 per cent of all the matter) subsequently begin to fall into the pre-existing gravitational potential wells of the dark matter. In this regime we evolve the coupled collapse of the dark matter and the baryons, both evolving under their mutual gravity but with different initial conditions. We find that a halo destined to contain the first observable star in the Universe reaches a δ∼ 1 per cent at z∼ 10⁶ and grows to δ∼ 6 per cent at matter–radiation equality and δ∼ 13 per cent at cosmic recombination. As the fluctuation enters the horizon very early in the radiation-dominated era, the final value of δ_c(M, z) for a given M and z is insensitive to the precise starting redshift (as long as it is much higher than equality) or the precise treatment of the fluctuation's horizon crossing.

Figure 1

Open in new tabDownload slide

Evolution of the fractional overdensity δ for a spherical region containing 10⁵ M_⊙ that collapses at z= 66. We show the fully non-linear δ (solid curve) and the linearly extrapolated δ (dashed curve). We indicate the redshifts of halo collapse (z_coll), cosmic recombination (z_rec), matter–radiation equality (z_eq), and entry into the horizon (z_enter).

We find that δ_c is essentially independent of M, and for our assumed parameters it is lower than the EdS value by ∼1 per cent × (1 +z)/20 in the range z= 9–80. Adding the contribution of the radiation to the expansion of the Universe, as well as adding the baryon–photon coupling to the collapse, both reduce the extrapolated linear perturbation at collapse δ_c compared with the EdS value. These added physical effects reduce the collapse efficiency as only the dark matter component takes part in the collapse throughout. The radiation is kept smooth by its own pressure and it never participates in the collapse, while the baryons only gradually recover from their coupling to the photons and begin to catch up to the dark matter; during this recovery stage, as long as the baryon perturbations remain much smaller than those of the dark matter, the baryons essentially do not participate in the collapse. Now, any reduction in the matter fraction that collapses (compared to 100 per cent in the usually assumed case of pure cold dark matter) depresses the linear evolution of the density perturbation more strongly, while the non-linear perturbation is larger and is thus less affected by the components that do not help in the collapse. Therefore the linear perturbation reaches a lower value of δ_c when the non-linear perturbation collapses. Note that while the change in δ_c may seem small, when dealing with rare haloes, even a change of a few per cent in δ_c can change the halo abundance at a given redshift by an order of magnitude (Fig. 2). Even at redshift 20, the 1 per cent change in δ_c compared to its previously assumed value changes the cumulative halo mass function n(>M) by ≳10 per cent.

Figure 2

Open in new tabDownload slide

Cumulative halo mass function n(>M). At z= 66 (top panel) we compare our full result for n(>M) (solid curve) to that resulting from adopting the EdS value of δ_c= 1.686 (dashed curve). At z= 20 (bottom panel), we show the relative error in n(>M) that results from using δ_c= 1.686 instead of our full result.

4 Statistical Considerations

As noted earlier, the minimum halo mass that can form a star at high redshift is determined by H₂ cooling (Tegmark et al. 1997). Numerical simulations (Abel et al. 2002; Bromm et al. 2002; Fuller & Couchman 2000; Yoshida et al. 2003; Reed et al. 2005) imply a minimum circular velocity V_c∼ 4.5 km s⁻¹, where 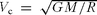in terms of the halo virial radius R. This yields a corresponding minimum mass at each redshift z′, M_min(z′). The simulations show that in a halo above the minimum mass, the gas cools in the dense centre and forms at least one star very quickly; this is understood theoretically as both the cooling time and the dynamical time are a small fraction of the cosmic age at that time.

Given the comoving number density of such star-forming haloes at each redshift, n[M_min(z′), z′], the mean expected number of star-forming haloes observed at redshift z or higher is

1

where dV is the comoving volume of the spherical shell in the redshift range z′ to z′+ dz′. Our results are independent of the adopted maximum redshift as long as z_max > 80. Although the mean expected number 〈N〉 (z) is determined theoretically by the cosmological parameters, in practice our observable Universe presents us with a single instance and the actual observed redshift is subject to Poisson and density fluctuations.

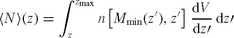
The effect of Poisson fluctuations is easily calculated. The chance of observing at least one star-forming halo above redshift z with Poisson fluctuations included is 1 − exp[−〈N〉 (z)], which yields a spread in the redshift of the first such halo of Δz≈ 3 at 1σ. In addition, the effect of density fluctuations on all scales is included statistically in our analytical model for the mean halo abundance at each redshift, but the correlations in the halo abundance between nearby points are not properly included. In other words, our calculation assumes that the relevant redshift shell gives us a fair sample of the density fluctuations on all scales. We first note that theoretically we expect that if we included the fully correlated density field, the effect on the predicted redshift of the first star-formation halo would be much smaller than the spread we find due to Poisson fluctuations. Because the Universe is homogeneous on large scales, large-scale modes can shift the halo abundance 〈N〉 (z) only by a small Δz; indeed, only 10 Mpc scales and smaller can produce a Δz > 1 (Barkana & Loeb 2004). Such small-scale modes are indeed very well sampled within the spherical redshift shells that have a very large radius of ∼12 500 Mpc. We have also verified this with a direct quantitative test. We have used the power spectrum to produce instances of the full, correlated density field in three-dimensional boxes. We have then modified the abundance n[M_min(z), z], increasing it in high-density regions and decreasing it in low-density regions according to a model that fits the results of numerical simulations (Barkana & Loeb 2004). In a 1-Gpc³ box resolved into 256³ cells, we found that including a correlated density field shifts the typical redshift of the first star-forming halo in the box by a Δz < 1, which is already a smaller effect than the Poisson redshift spread. The spherical shells in the real Universe have a larger volume by a factor of ∼2000, so the density fluctuations are far better sampled than in our 1 Gpc³ box, and the effect of the correlations on the redshift of the first star-forming halo in the Universe is negligible.

5 Predictions

The most likely redshift for the first observable star is 65.4 (Fig. 3), while the median redshift at which there is a 50 per cent chance of seeing the first star is 65.8, which corresponds to a cosmic age of t= 31 Myr, less than a quarter of one per cent of the current age of 13.7 Gyr. The 1σ (68 per cent) range is z= 64.7–67.3 (or t= 30–32 Myr) and the 2σ (95 per cent) range is z= 63.9–69.4. Note that even an error in the minimum V_c as large as a factor of 1.5 would cause only a 9 per cent change in the expected formation redshift. Note also that in terms of the total cosmic mass fraction contained in such haloes, the first star-forming halo corresponds to an 8.3σ density fluctuation on the mass scale of 10⁵ M_⊙. Future simulations will allow us to check the validity of extrapolating the Sheth & Tormen (1999) halo mass function to such rare fluctuations.

Figure 3

Open in new tabDownload slide

The probability of finding the first star as a function of redshift. Vertical lines show the median redshift as well as the central 1σ (68 per cent) range and 2σ (95 per cent) range.

We can consider a similar question for other populations of haloes (Fig. 4). For example, the radiation from the first stars is expected to eventually dissociate all the H₂ in the intergalactic medium, leading to the domination of a second generation of larger galactic haloes where the gas cools via radiative transitions in atomic hydrogen and helium (Haiman, Rees & Loeb 1997). Atomic cooling occurs in haloes with V_c > 16.5 km s⁻¹, in which the infalling gas is heated above 10 000 K and is ionized. We find that the first galaxy to form via atomic cooling formed at z= 46.6^+1.2_−0.9, which corresponds to t= 52⁺¹₋₂ Myr, where we have indicated the median values and 1σ ranges. We also predict that the first halo as large as that of our own Milky Way galaxy (Battaglia et al. 2005) formed at z= 11.1^+0.5_−0.2, or t= 408⁺¹⁵₋₂₀ Myr. Also, the first halo with the mass of the Coma galaxy cluster (Lokas & Mamon 2003) formed at z= 1.24^+0.14_−0.10, or t= 5.0 ± 0.4 Gyr.

Figure 4

Open in new tabDownload slide

The median redshift for the first appearance of various populations of haloes. We consider haloes above a minimum circular velocity (left-hand panel) or minimum mass (right-hand panel). We indicate in particular the first star-forming halo in which H₂ allows the gas to cool, the first galaxy that forms via atomic cooling (H), as well as the first galaxy as massive as our own Milky Way and the first cluster as massive as Coma. The horizontal lines indicate the elapsed time since the big bang. We compare the results with the cosmological parameters from Spergel et al. (2006) (solid curve) to those with the parameters from Viel et al. (2006) (dashed curve); the difference represents roughly the systematic 1σ error due to current uncertainties in the values of the cosmological parameters.

6 Discussion

There remains a ∼10 per cent systematic uncertainty in the above 1 +z values due to current uncertainties in the cosmological parameters. Varying the cosmological parameters has a negligible effect on the critical overdensity (δ_c) but significantly changes the power spectrum and also the spatial scale corresponding to a given halo mass or circular velocity. We illustrate the uncertainties in Fig. 4 using the alternate cosmological parameters from Viel, Haehnelt & Lewis (2006): Ω_m= 0.253, Ω_Λ= 0.747, Ω_b= 0.0425, h= 0.723, n= 0.957 and σ₈= 0.785. These parameters also represent typical 1σ errors, in terms of the parameters uncertainties given by Spergel et al. (2006). We obtained for these alternate parameters that the first star formed at z= 60.0, which represents a 9 per cent reduction in 1 +z compared to our standard parameters; also the value of 1 +z is lowered by 9 per cent for the first atomic-cooling halo, 7 per cent for the first Milky Way mass halo, and 8 per cent for the first Coma mass cluster.

On the other hand, astrophysical uncertainties about metallicity and feedback can only affect the precise properties of a halo of a given mass, but not whether or not it forms. Also, in a halo with a short cooling time, processes within the halo should not induce a significant uncertainty in the formation time of the first stars within it, as a halo virializes at a density of ∼180 times the cosmic mean density, and so the gravitational dynamical time within it is always smaller than the age of the Universe at the time by at least an order of magnitude. Because the baryonic component collapses by another factor of ∼20 until the collapse is halted by angular momentum (assuming a typical halo spin parameter of ∼5 per cent; see, e.g. Mo, Mao & White 1998), the dynamical time within a disc or a star-forming region is likely to be shorter still by another two orders of magnitude.

In summary, by accounting for the size of the observable Universe as well as the early cosmic history of individual haloes (Fig. 1), our results extend the era of star formation much earlier than current simulations suggest. An analytical model of galaxy formation that has been normalized to simulation results allows us to predict the earliest time that various halo populations can be observed (Fig. 4). Because the statistical uncertainty in this time is dominated by Poisson fluctuations, we can analytically predict its full probability distribution (Fig. 3). Our results also show that in order to numerically simulate galaxy formation accurately at z≥ 20, current simulation methods must be revised to include the effect on a forming halo of the early cosmic history of radiation and baryons. Simulations that neglect this, even if they overcome the statistical challenges by covering the volume of the entire observable Universe, will underestimate the number of haloes at z= 20 (Fig. 2) by 9 per cent for all haloes above the H₂ cooling threshold (6 × 10⁵ M_⊙ at z= 20), and by 15 per cent for all haloes above the atomic cooling threshold (3 × 10⁷ M_⊙ at z= 20).

Acknowledgments

The authors acknowledge support by Israel Science Foundation grant 629/05 and US – Israel Binational Science Foundation grant 2004386.

References